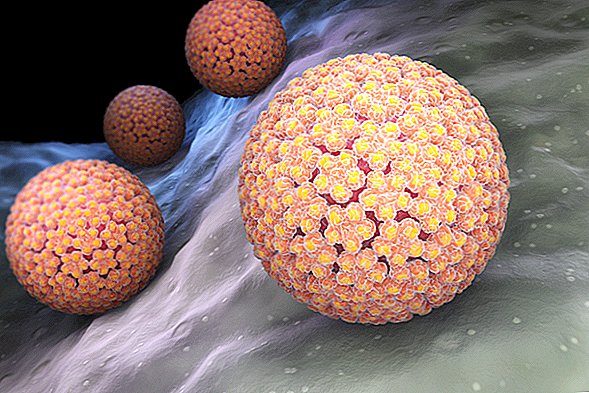
Billedtekst: Udsigt til månen ved perigee og apogee
Som lærer er jeg altid på udkig efter laboratorier med enkle opsætninger, der passer til studerende. Min nuværende favorit er at finde lysets hastighed med chokolade.
I en ny artikel, der for nylig blev uploadet til arXiv, beskriver Kevin Krisciunas fra Texas A&M en metode til at bestemme månens orbitaleksentricitet med en overraskende lav fejl ved ikke at bruge noget mere end en meterpind, et stykke pap og et program beregnet til montering af kurver til variable stjerner.
Denne metode gør brug af det faktum, at excentriciteten kan bestemmes ud fra forholdet mellem den gennemsnitlige vinkelstørrelse af et objekt og halvdelen af dets amplitude. Hovedmålet er således at måle disse to mængder.
Kevins strategi for at gøre dette er at gøre brug af et karton til syne, der kan glide langs en meterstokk. Ved at kigge gennem hullet på månen og skubbe kortet frem og tilbage, indtil hullets vinkelstørrelse bare overlapper månen. Derefter giver hullets diameter divideret med afstanden nede på målepinden vinkelstørrelsen takket være den lille vinkelformel (? = D / D i radianer hvis D >> d).
For at forhindre systematiske fejl ved fejlvurdering, når kortet glider frem, indtil hullets størrelse matcher månen, er det bedst at også nærme sig det fra den anden retning; Kommer ind fra den yderste ende af måleren. Dette skulle hjælpe med at reducere fejl, og i Kevin's forsøg fandt han, at han havde en typisk spredning på ± 4 mm, når han gjorde det.
På dette tidspunkt er der endnu en systematisk fejl, der skal tages i betragtning: Eleven har en endelig størrelse, der kan sammenlignes med synshullet. Dette undervurderer den faktiske vinkelstørrelse. Som sådan er en korrektionsfaktor nødvendig.
For at udlede denne korrektionsfaktor placerede Kevin en 91 mm disk i en afstand af 10 meter (dette skulle producere en disk med samme vinkelstørrelse som månen, når den ses fra denne afstand). For at producere den bedste match, glip af karton med synshullet skulle gerne skal placeres på 681,3 mm på måleren, men på grund af den systematiske fejl fra eleven fandt Kevin, at det var nødvendigt at placere det på 821 mm. Forholdet mellem den observerede placering og den korrekte placering tilvejebragte korrektionsfaktoren Kevin anvendte (1.205). Dette skal kalibreres for hver enkelt person og vil også afhænge af lysmængden i løbet af observationstiden, da dette også påvirker pupillens diameter. Imidlertid giver vedtagelse af en enkelt korrektionsfaktor tilfredsstillende resultater.
Dette tillader korrekt taget data, som derefter kan bruges til at bestemme de nødvendige mængder (den gennemsnitlige vinkelstørrelse og 1/2 amplituden). For at bestemme disse brugte Kevin et program kendt som PERDET, som er designet til montering af sinusformede kurver til svingninger i variable stjerner. Ethvert program, der kunne passe sådanne kurver til datapunkter ved hjælp af en?2 fit eller en Fourier-analyse ville være passende til dette formål.
Fra sådanne programmer, når den gennemsnitlige vinkelstørrelse og halvamplitude er bestemt, giver deres forhold excentriciteten. For Kevins eksperiment fandt han en værdi på 0,039 ± 0,006. Derudover var den periode, han bestemte fra perigee til perigee, 27,24 ± 0,29 dage, hvilket er i fremragende overensstemmelse med den accepterede værdi på 27,55 dage.