Gravitationsbølger er tilsyneladende djævelsk vanskelige ting at modellere med Einstein-feltligninger, da de er meget dynamiske og ikke-symmetriske. Traditionelt var den eneste måde at komme tæt på at forudsige de sandsynlige virkninger af tyngdekraftsbølger på at estimere de krævede Einstein-ligningsparametre ved at antage, at objekterne, der forårsager tyngdekraftsbølgerne, ikke genererede stærke tyngdekraftfelter i sig selv - og heller ikke bevægede sig med hastigheder overalt i nærheden af lysets hastighed.
Problemet er, at de mest sandsynlige kandidatobjekter, der muligvis genererer påviselige tyngdekraftsbølger - tæt binære neutronstjerner og fusionerende sorte huller - har nøjagtigt disse egenskaber. De er meget kompakte, meget massive kroppe, der ofte bevæger sig med relativistiske (dvs. tæt på lysets hastighed) hastigheder.
Er det ikke underligt, at den 'guesstimate' tilgang, der er beskrevet ovenfor, faktisk fungerer strålende med at forudsige adfærden ved tæt massive binære grupper og sammenlægning af sorte huller. Derfor et nyligt papir med titlen: Om den urimelige effektivitet af post-Newtonian tilnærmelse i gravitationsfysik.
Så for det første har ingen endnu registreret tyngdekraftsbølger. Men selv i 1916 vurderede Einstein deres eksistens som sandsynligt og demonstrerede matematisk, at gravitationsstråling skulle opstå, når du erstatter en sfærisk masse med en roterende håndvægt med samme masse, som på grund af dens geometri vil generere dynamiske ebbe- og strømningseffekter på rummet når det roterer.
For at teste Einsteins teori er det nødvendigt at designe meget følsomt detekteringsudstyr - og indtil videre har alle sådanne forsøg mislykkedes. Yderligere håb hviler nu stort set på laserinterferometer rumantennen (LISA), som ikke forventes at blive lanceret før 2025.

Dog såvel som følsomt detektionsudstyr som LISA, er du også nødt til at beregne, hvilken slags fænomener og hvilken slags data der repræsenterer et definitivt bevis på en tyngdekraftbølge - som er her, all den teori og matematik, der kræves for at bestemme disse forventes værdier er afgørende.
Oprindeligt udarbejdede teoretikere a post-newtonsk (dvs. Einstein-æraen) tilnærmelse (dvs. guesstimate) for et roterende binært system - selvom det blev erkendt, at denne tilnærmelse kun ville fungere effektivt for et system med lav masse, lav hastighed - hvor enhver komplicerende relativistiske og tidevandseffekt, der skyldes selvtyngdekraften og hastigheden af de binære objekter sig selv, kunne ignoreres.
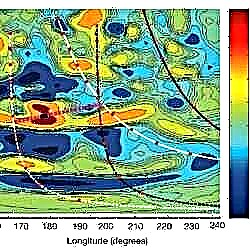
Derefter kom æraen med numerisk relativitet, hvor fremkomsten af supercomputere gjorde det muligt at faktisk modellere alle dynamikken i tæt massive binære bevægelser med relativistiske hastigheder, ligesom hvordan supercomputere kan modellere meget dynamiske vejrsystemer på Jorden.
Overraskende, eller hvis du vil urimeligt, de beregnede værdier fra den numeriske relativitet var næsten identiske med dem, der blev beregnet ved den angiveligt kropsfulde post-Newtonian tilnærmelse. Den post-Newtonian tilnærmelsesmetode er ikke meningen, at den skal fungere i disse situationer.
Alt, hvad forfatterne sidder med, er muligheden for, at gravitationsrødskift får processer nær meget massive genstande til at virke langsommere og gravitationsmæssigt 'svagere' for en ekstern observatør, end de virkelig er. Det kunne - slags, slags - forklare den urimelige effektivitet ... men kun slags, slags.
Yderligere læsning: Will, C. Om den urimelige effektivitet af den post-Newtonian tilnærmelse i gravitationsfysikken.